[Arithmétique] - [Affichage] - [Addition] - [Soustraction] - [Multiplication] - [Division]

.:: Rubrique Arithmétique >> Addition ::.

Maintenant passons aux choses sérieuses... l'addition ! vous êtes prêt? c'est parti
Etudions d'abord la méthode de résolution d'une addition qu'on apprend en primaire: un petit exemple pour commencer? oui mais en héxadécimal:

1

1

1

 

 

 

 

 

 

E

5

h

+

F

F

4

3

h

1

0

0

2

8

h

|=> 0xE5+0xFF43=0x10028

ça parait tout simple comme ça? et bien on va voir... il suffit de traduire cet algorithme en assembleur:

Déjà on définit nos deux nombres _NOMBRE1 et _NOMBRE2:
_NOMBRE1 = 0xE5
_NOMBRE2 = 0xFF43

On considère pour simplifier les choses que _NOMBRE2 est le nombre le plus grand.

De plus, il va falloir enregistrer le résultat dans une variable on va choisir la variable _NOMBRE2 car c'est celle qui nécessite le plus de mémoire. Le résultat va donc écraser la valeur initiale de _NOMBRE2 et pour ne pas avoir de problème de conflit (car le résultat sera d'au maximum un quartet plus long que _NOMBRE2) on alloue à _NOMBRE2 un octet suplémentaire.

Mais que se PASTIS? je RICARD KRONENBOURG LABEL...

Ce qui nous donne en assembleur:

	_NOMBRE1:
	
		db 0x01		;Longueur du nombre1 en octet (LONG)
		db 0xE5		;Le nombre1 (DATA)
	
	_NOMBRE2:
	
		db 0x02		;Longueur du nombre2 en octet (LONG)
		db 0x43, 0xFF 	;Le nombre2 (DATA)
		db 0x00		;L'octet suplémentaire

 Maintenant passons a l'algorithme:

|- * On initialise p à 0 (ce sera notre compteur);
|- * On initialise r à 0 (ce sera notre retenu);
|- * On boucle tant que p < min(_NBR1.LONG, _NBR2.LONG)
____|- * s = ((BYTE)_NBR1.DATA[p]) + ((BYTE)_NBR2.DATA[p]) + r;
____|- * r = octet de poids fort de s;
____|- * On incrémente p;
|- * On ajuste la somme si _NBR1.LONG != _NBR2.LONG;
|- * On ajoute le reste final;

Ce qui donne... traduit en asm:

	_ADDITION:
	
		mov di, _NOMBRE1 	;on pointe avec di sur l'offset de _NOMBRE1
		mov ch, [ds:di] 	;on récupère la longueur du nombre le plus court qui va nous servir de compteur
		mov si, _NOMBRE2 	;on pointe avec si sur l'offset de _NOMBRE2
		mov cl, [ds:si] 	;on récupère la longueur du nombre le plus long qui va nous servir de compteur
		xor dx, dx 		;registre qui nous servira pour stocker la retenue.
		xor bx, bx
		
	_BOUCLE_ADD:
	
		inc di
		inc si
		xor ax, ax
		
		test ch, ch 		;on teste si ch == 0
		je _SUITE_ADD 		;si oui on saute
		
		dec ch
		mov al, [ds:di] 	;valeur d'un octet de _NOMBRE1
		
	_SUITE_ADD:
	
		mov bl, [ds:si] 	;valeur d'un octet de _NOMBRE2
		add ax, bx
		add ax, dx 		;on additionne ax et la retenue
		mov dl, ah 		;on récupère la retenue
		mov [ds:si], al 	;on sauve la nouvelle valeur de al
		
		dec cl
		test cl, cl 		;on teste si cl != 0
		jne _BOUCLE_ADD 	;si oui on saute
		
		test dl, dl 		;on teste si dl != 0
		jne _RETENUE_ADD 	;si oui on saute
		
		ret 			;si non on retourne au programme principal
		
	_RETENUE_ADD:
	
		inc si
		mov [ds:si], dl 	;on sauve la retenue dl
		
		mov si, _NOMBRE2 	;on pointe avec si sur l'offset de _NOMBRE2
		mov cl, [ds:si] 	;on récupère la longueur du nombre le plus long qui va nous servir de compteur
		inc cl
		mov [ds:si], cl 	;on sauve la nouvelle longueur de _NOMBRE2
		
		ret

Et maintenant un petit test pour vérifier: (je n'ai pas pris les mêmes nombres que l'exemple pour vous montrer que ça marche très bien pour des grands nombres)

_NOMBRE1 = 0123456789ABCDEF (16 chiffres)
et
_NOMBRE2 = 0FEDCBA9876543210FEDCBA987654321 (32 chiffres)

Amusez-vous à calculer ça avec la calculette de WINDOWS... on peut pas.

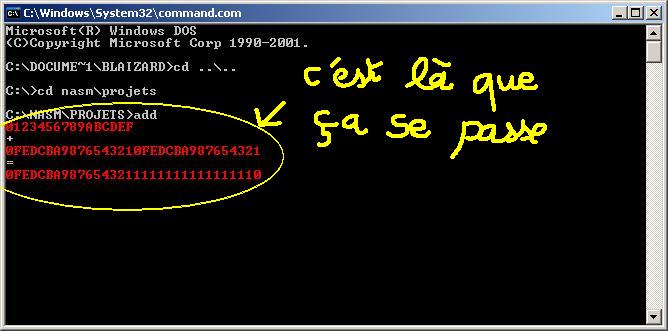
Le compte est bon !!!!

Et voilà c'est terminé pour l'addition... demain, la multiplication ?... non?

Voici les différentes rubriques:

Daemonium Albus,
blaizard@caramail.com