[Arithmétique] - [Affichage] - [Addition] - [Soustraction] - [Multiplication] - [Division]

.:: Rubrique Arithmétique >> Division ::.

Comment on divise deux nombres?
J'ai 3 méthodes à vous proposer:

  1. La méthode classique (scolaire):
    en gros c'est la méthode qu'on apprend à l'école. Je ne vais pas vous faire un dessin, je suis sur que vous vous rappelez ces formidables heures de maths à faire des divisions...
  2. La méthode bidouillage:
    le but est de faire la somme du dénominateur jusqu'à ce que cette somme soit supérieure ou égale au nominateur. On trouve le résultat en comptant le nombre de fois qu'on à fait cette somme - 1.
    Un petit exemple:
    n=7000 et d=1234, on cherche q=n/d, normalement on devrait trouvé q=5 (on cherche la valeur entière).
    Et c'est parti !
    1. 0+1234 < n
    2. 1234+1234=2468 < n
    3. 2468+1234=3702 < n
    4. 3702+1234=4936 < n
    5. 4936+1234=6170 < n
    6. 6170+1234=7404 > n
    donc on s'arrête et on compte le nombre de fois qu'on à sommé d, ici 6 fois, on retranche 1 et on trouve le bon résultat.
  3. La méthode "de Newton":
    Le but est de remarquer que diviser un nombre par un autre revient à le multiplier par l'inverse de cet autre nombre.
    Oui mais comment on calcule l'inverse d'un nombre? et bien on utilise l'algorithme de Newton pardi! là on se dit qu'il n'est pas mort pour rien.
    Et voici ce que vous attendez tous... rapide et ingénieux... j'ai nommé... l'algorithme de Newton !!!
    c'est en fait une suite récurente de la forme:

    xn+1=2*xn-a*xn²

    avec a qui est le nombre à inverser, quand n tend vers l'infini, xn tend vers 1/a. Et donc une fois qu'on a une approximation correcte de 1/a, il suffit de multiplier 1/a par le nominateur et c'est gagné!
    Mais ya juste un p'tit problème: il faut partir d'une valeur de x0 qui ne soit pas trop éloigné du résultat pour rendre le calcul rapide. On réfléchit...
    a<10a.longueur
    1/a>10-a.longueur
    donc on peut poser x0 = 10-a.longueur.

mais que faire de tout ça ???!!!!

Et bien don't panic!, une bonne méthode est d'utiliser la méthode 3 en la combinant avec la seconde méthode:
Pour une division du type b/a, on cherche d'abord une valeur approchée de 1/a, on la multiplie par b puis on ajuste cette valeur grâce à la méthode 2.

Ce qui devrait donner algorithmiquement pour b/a:

|- * On pose x0 = 10-a.longueur;
|- * On calcule xn jusqu'à ce qu'on trouve une valeur de xn ~ xn-1;
|- * On multiplie xn par b et on sauve cette valeur dans Q (le quotient);
|- * On pose R = Q*a; ce qui sera notre valeur initiale pour la méthode 2 et qui devrait être relativement proche de b.
-------Si R > b------------------------ -------Sinon---------------------------
|- * On boucle tant que R > b |- * On boucle tant que R < b
____|- * R reçoit R - a; ____|- * R reçoit R + a;
____|- * Q reçoit Q - 1; ____|- * Q reçoit Q + 1;
|- * Si R != a
____|- * Q reçoit Q - 1;
|- * On affiche Q, qui est le résultat, si on veut :-)

On commence donc par calculer une approximation de 1/a par l'algorithme de newton,
Comme nos nombres sont des entiers uniquement, on va calculer 1/a*(X+4) avec X une puissance de 16 car on travaille en hexa et +4 car on va enregistrer le résultat obtenu dans un registre 16 bits. Passons au code: 

	_ALGO_NEWTON:	
		;on récupère la longueur exacte du nombre 
		;et non la longueur du nombre à +-1 chiffre près
		xor ax, ax
		mov si, _NOMBRE2
		mov al, [ds:si]
		add si, ax
		shl ax, 1
		mov cl, [ds:si]
		test cl, 0xF0
		je _IMPAIRE1			;saute si le nombre est paire
		inc ax
	_IMPAIRE1:				;récupère la taille exacte de _NOMBRE2 dans ax
		push ax			;on empile TAILLE_NOMBRE2
	
		mov cx, 0x10			;0x10 est ici x0
	_BOUCLENEWTON:
		push cx
		
		mov al, cl
		mov bl, al
		mul bl			;ax=bl² on obitent donc ici xn²
		mov si, _MEM2			;_MEM2 est les donnés du nombre temporaire (il est définit sur 3 octets 
						;c'est donc un stockage sur 16 bits)
		mov [ds:si], ax
	    	push word _NOMBRE3		;[sp-4] => résultat
	    	push word _NOMBRE2		;[sp-2]
	    	push word _MEM		;[sp] _MEM est le nombre qui contient les données _MEM2
	    	call _MULTIPLICATION		;on multiplie xn² par a
	    	add sp, 6			;pour "supprimer" de la pile les arguments envoyés à _MULTIPLICATION
	
		pop cx
		
		;recupère dans ax le résultat de la division
		;et ajuste sa longueur
		pop bx			;récupère TAILLE_NOMBRE2
		push bx
		mov si, _NOMBRE3
		inc si
		shr bx, 1			;divise TAILLE_NOMBRE2 par 2
		jnc _PAIRE1
		add si, bx
		mov ax, [ds:si]
		shr ax, 4
		jmp _SUITEPAIRE1
	_PAIRE1:
		add si, bx
		mov ax, [ds:si]
	_SUITEPAIRE1:
	
		mov dx, cx			;sauve dans dx la valeur de x(n-1)
		shl cx, 1			;multiplie cx par 2
		sub cx, ax			;cx contient ici une approximation de 1/_NOMBRE2
		mov bx, cx
		shr bl, 1
		shr dl, 1
		cmp bl, dl			;boucle tant que x(n-1) != x(n)
		jne _BOUCLENEWTON
	; en sortie cx contient une approximation de 1/_NOMBRE2 et la pile contient TAILLE_NOMBRE2

Voilà maintenant qu'on a une approximation de 1/a il va falloir passer à la phase 2 de l'algo:
"La 2ème méthode" (je ne lui est pas encore trouvé de nom, si vous avez des idées de nom ou bien si cet algorithme en porte déjà un vous pouvez me faire parvenir vos idées par mail, merci d'avance je sais que c'est pas le moment mais y a t'il quelqu'un qui vendrait un narguilé avec 4 embouts et pour moins de 100 euros? idem, repondez moi, ça parait pas mais c'est sérieux.)
Bon, où en étais-je?
ah oui, la 2ème méthode...on va devoir multiplier b par l'approximation de 1/a puis multiplier cette valeur par le "vrai" a et enfin sauver ce nombre. Ce qui se traduit par de l'assembleur à peu près comme ça: 

		;cx contient une approximation de 1/_NOMBRE2 et la pile contient TAILLE_NOMBRE2
		mov si, _MEM2
		mov [ds:si], cx
		
	    	push word _NOMBRE3	;[sp-4] => résultat
	    	push word _NOMBRE1	;[sp-2]
	    	push word _MEM		;[sp]
	    	call _MULTIPLICATION	;On multiplie b par 1/a et on sauve le résultat dans _NOMBRE3
	    	add sp, 6
	
		pop ax
		push ax
		
		;maitenant il faut ajuster la longueur du resultat car on avait multipilier le nombre
		;précédent par une puissance de 16 pour se débarasser de la virgule
		mov si, _NOMBRE3
		mov cl, [ds:si]
		inc si
		mov di, si
		shr cl, 1
		shr ax, 1
		jnc _PAIRE2
		add si, ax
	_SUITEDIV1:
		mov ax, [ds:si]
		shr ax, 4
		mov [ds:di], ax
		add si, 2
		add di, 2
		dec cl
		test cl, cl
		jne _SUITEDIV1
		jmp _FINDIV
	_PAIRE2:
		add si, ax
	_SUITEDIV2:
		mov ax, [ds:si]
		mov [ds:di], ax
		add si, 2
		add di, 2
		dec cl
		test cl, cl
		jne _SUITEDIV2
	_FINDIV:
		pop bx
		xor cx, cx
		mov si, _NOMBRE3
		mov di, si
		mov cl, [ds:si]
		shr bx, 1
		sub cl, bl
	        add di, cx
	        mov al, [ds:di]
	        test al, al
	        jne _SUITEDIV3
	        dec cl
	_SUITEDIV3:
		mov [ds:si], cl
		;Fiiiooouuuuffffff.... on a terminé d'ajuster la longueur du résultat.
		;On doit probablement pouvoir trouver une méthode plus rapide mais comme
		;cette partie de code ne contient qu'une petite boucle elle est très rapidement exécuté.
		;(2 boucle en fait mais le prog ne passera que par une des 2 suivant la parité d'un nombre)
		xor cx, cx
		mov si, _NOMBRE3
		mov cl, [ds:si]
		inc si
		add si, cx		;si contient l'adresse du nombre temporaire
		;ce nombre temporaire est R
		;il va être comparé à b pour ajuster la valeur du quotient
	    	mov di, _NOMBRE1	;initialise le nombre temporaire
	    	mov cl, [es:di]
	    	mov di, si
	    	inc di
	    	xor ax, ax
	    	rep stosb
		
	    	push si		       	;[sp-4] => résultat
	    	push word _NOMBRE3      	;[sp-2]
	    	push word _NOMBRE2     	;[sp]
	    	call _MULTIPLICATION
	    	add sp, 6
	    	
	    	mov di, _NOMBRE1	;initialise la longueur du nombre temporaire
	    	mov cl, [es:di]
	    	mov [ds:si], cl

C'est pas plus compliqué que ça :-)
Maintenant il ne vous reste plus qu'à faire la boucle pour ajuster la valeur et c'est gagné.
je vais quand même vous aider un peu, je vous ai fait la fonction qui permet de comparer deux nombre (c'est un peu prise de tête , alors merci qui?).
ça c'est cadeau: 

	_CMP:
		xor cx, cx
		xor dl, dl
		mov cl, [ds:di]		;cx contient la taille de NOMBRE1
		add si, cx
		add di, cx
	_BOUCLE_CMP:
		mov al, [ds:di]		;al contient NOMBRE1
		mov bl, [ds:si]		;bl contient NOMBRE2
		dec si
		dec di
		test cx, cx
		je _DI_SUP_SI
		dec cx
		cmp al, bl
		je _BOUCLE_CMP		;reboucle si NOMBRE1 == NOMBRE2
		
		cmp al, bl
		jc _DI_INF_SI			;saute si NOMBRE1 < NOMBRE2
	
	_DI_SUP_SI:
	        jmp _CMP_SUITE		;lorsqu'on reboucle
	_DI_INF_SI:
		jmp _FIN_DIVI			;quand le on tient l'bon quotient

Puis on teste le programme final:

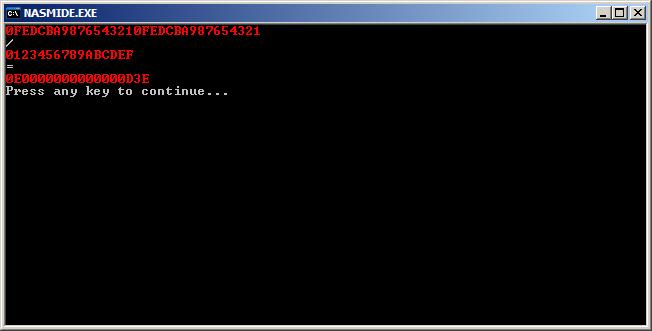
C'est bon !!!
YYYYYYYEEEEEEEEEEEAAAAAAAAAAAAAAAAAAHHHHHHHHHHHHHHHHHHHHH !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Et voilà c'est terminé pour la division et pour cette rubrique aussi... une petite larme?
Si vous êtes courageux vous pouvez vous amuser à coder des logarithmes & co pour le plaisir pour ça je vous conseille de jeter un coup d'oeil sur les séries entières.

Bon code et bon hack/crack :-)

Voici les différentes rubriques:

Daemonium Albus,
blaizard@caramail.com