.:: Rubrique Arithmétique >> Multiplication ::.

J'espère que vous avez bien compris l'addition! sinon un petit conseil, rebroussez chemin! niark !!!

Bon, comment partir?
On s'inspire de la méthode qu'on utilise pour multiplier deux nombres entre eux (je ne parle pas bien sûr de la calculatrice ).
Prenons un exemple simple pour commencer: 6789*7

=(6000+700+80+9)*7

=(6*7)*1000+(7*7)*100+(8*7)*10+9*7

=42000+4900+560+63

=47523

Donc on tout d'abord, on crée un nombre R qui a pour valeur 0.
Ensuite on multiplie le chiffre de poids faible par 7 et on le met dans R. R=63
On fait de même pour le chiffre suivant (8*7) et on le multiplie par 10 (car on travaille pour cet exemple en base 10) avant de l'ajouter à R. R=623
IDEM pour le suivant (7*7), on le multiplie par 100 et on l'ajoute à R. R=5523
Et enfin on multiplie le chiffre de poids fort par 6, on le multiplie par 1000 et on l'ajoute à R. R=47523

Ouahou !!!! super !!! Mais comment on fait pour multiplier un nombre par un autre nombre et non plus par un chiffre ?
et bien on décompose les 2 nombres:
soit 6789*2345

=(6000+700+80+9)*(2000+300+40+5)

=[(6*5)*1000+(7*5)*100+(8*5)*10+(9*5)]
+[(6*4)*1000+(7*4)*100+(8*4)*10+(9*4)]*10
+[(6*3)*1000+(7*3)*100+(8*3)*10+(9*3)]*100
+[(6*2)*1000+(7*2)*100+(8*2)*10+(9*2)]*1000

=6789*5
+6789*4*10
+6789*3*100
+6789*2*1000

=...

=15920205

En fait c'est le même principe que précédemment, sauf qu'on effectue des "pseudos multiplications" et on les additionne ensuite en les multipliant successivement par 10, 100, 1000, ...
voilà vous connaissez tout sur la multiplication des grands nombres en base 10.
Pour des nombres héxadécimaux, c'est exactement le même principe sauf q'au lieu de multiplier par 10 vous multipliez par 16 (sois 0x10 en héxa).
C'est en fait ça l'algorithme de mon programme, je vous laisse "déguster" le code-source:

Instructions x86	X

	_MULTIPLICATION:
		xor cx, cx
		xor bx, bx
		mov si, _NOMBRE1		;premier facteur
		mov cl, [ds:si]
		mov si, _NOMBRE2		;deuxième facteur
		mov bl, [ds:si]
		add cx, bx
		;ici cx contient la longueur max du resultat
		mov di, _NOMBRE3		;adresse du résultat
		mov [es:di], cx
		inc di
		xor ax, ax
		rep stosb			;on met le nombre qui fera office de résultat à 0
		
	
	_BOUCLEMUL2:
	
		push ax
	
		xor dx, dx
		xor cx, cx
		mov si, _NOMBRE2
		add si, ax
		inc si
		mov bl, [ds:si]		;bl contient un facteur
	
		mov si, _NOMBRE1
		mov bh, [ds:si]		;bh contient la longueur du nombre
	
		mov di, _NOMBRE3
		add di, ax
	
	_BOUCLEMUL1:				;boucle qui sert à effectuer les "pseudos multiplications"
		inc si			;et les additionner en même temps
		inc di
		xor ah, ah
		mov al, [ds:si]
		mul bl
		mov cl, [ds:di]
		add ax, cx
		add ax, dx
		mov dl, ah			;dl contient l'octet de retenue
		mov [ds:di], al
		dec bh
		test bh, bh
		jne _BOUCLEMUL1
	
		test dl, dl
		je _SUITENORET
	
		inc di
		mov cl, [ds:di]
		add dl, cl
		mov [ds:di], dl
	
	_SUITENORET:				;saute à ce label s'il n'y a pas de retenue dans le résultat
	
		pop ax
		inc ax
	    
		mov si, _NOMBRE2
		mov bl, [ds:si]
		cmp al, bl
		jne _BOUCLEMUL2
	
		mov si, _NOMBRE3
		mov ax, di
		sub ax, si
		mov [ds:si], al
	    
		ret
	

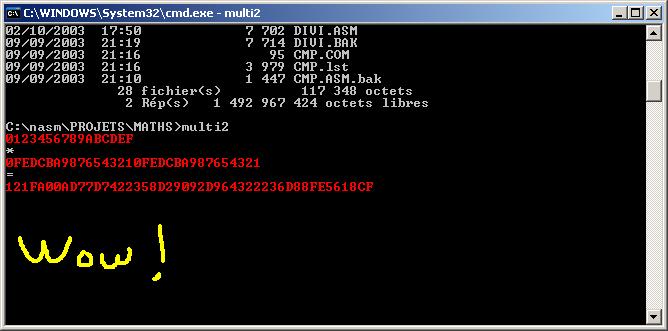
Plus qu'à mettre le programme à l'essai:

Voici les différentes rubriques:

• Instructions des x86.

• Arithmétique.
  • Affichage.
  • Addition.
  • Soustraction.
  • Multiplication.
  • Division.

Daemonium Albus,
blaizard@caramail.com